CPA 2: the CPAening

continuing to make some sort of sense out of side channel literature that is out there, here's another cool trick with actual code

one of the issues with doing time-domain side channel analysis is that all your traces need to be perfectly aligned. this can prove challenging, especially if the target has side channel countermeasures that include random delays in the sensitive code to throw off alignment. what can you do about that? well you could do your analysis in the frequency domain instead of the time domain

frequency domain?

typically side channel traces are a relation between time and the power consumption (or RF emanations) at that time. using a Fourier transform¹, this can be converted into a relation between various frequencies and their amplitude and phase (which when added together form the original signal²). the side channel leakage, at least for first order attacks, can still show itself in the frequency-domain version of the data, and thus can be extracted that way. the important thing is in the frequency domain we don't actually care about trace offset at all. trace alignment is irrelevant because in the frequency domain, the only difference between two signals that are identical but offset by some amount of time is the phase of the resulting frequency bins (and we ignore phase)

ok let's do it

first some probably familiar code if you've seen the previous post. we're using the ASCAD_desync100 dataset and taking 2000 traces out of that (also using the mask metadata)³

ntraces = 2000
db = h5py.File("./ASCAD_databases/ASCAD_desync100.h5", "r")["Attack_traces"]
traces = db["traces"][0:ntraces, :].astype("double")

logger.info("making first order model")
model = numpy.repeat(numpy.arange(256, dtype='uint8'), ntraces).reshape((256, ntraces))
for i in tqdm.trange(ntraces):
    (pt, ct, key, mask, desync) = db["metadata"][i]
    pt_v = pt[2]
    mask_v = mask[15]
    model[:, i] = AES_SBOX[model[:, i] ^ pt_v] ^ mask_v
model = numpy_popcount.popcount(model).astype("double").transpose()

ok now the fun part, transform all the traces with scipy.fft, take the absolute value of the result to discard phase information, and then take the top 50 peaks which we assume contain the leakage⁴

fft_traces = numpy.zeros(traces.shape, traces.dtype)
for i in range(traces.shape[0]):
    fft_traces[i, :] = numpy.abs(scipy.fft.fft(traces[i, :]))

traces = fft_traces[:, 1:350]
avg = numpy.mean(traces, axis=0)
peaks = avg.argsort()[-50:][::-1]
traces = numpy.hstack([traces[:, i:i+1] for i in peaks])

with this, do the typical correlation analysis as before, just like if traces represented the original time-domain trace set

correlator = Correlator(model)
coefs = correlator.corr_submatrix(traces)
coefs = numpy.abs(coefs)
max_by_key = numpy.max(coefs, axis=1)
plt.plot(max_by_key)
plt.show()

results

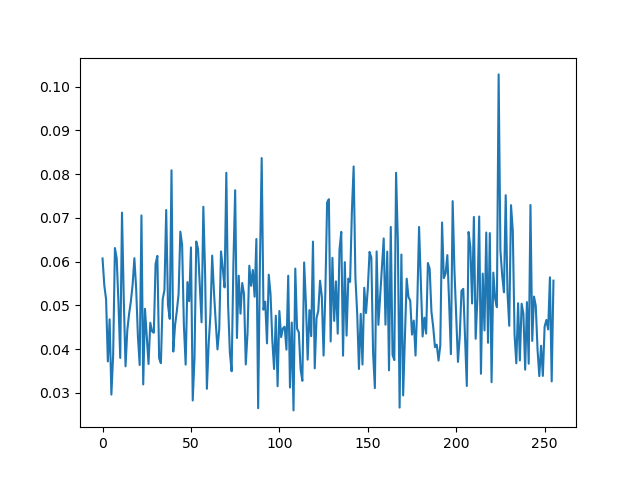
this is a lot more noisy than the time-domain attacks where we took care to align the traces, but the point is we still get the right key byte without any trace alignment being actually necessary, which makes this a really powerful kind of attack

the code (+ previous code) can be found here https://git.lain.faith/haskal/gist/src/branch/gist/sca/ascad/attack.py